Trợ giúp
Học tốt trên lớp
Luyện thi
Hiểu học hành
Trong bài viết này hãy cùng tìm hiểu về tam giác đồng dạng và các trường hợp đồng dạng của tam giác nhé!
Đây là kiến thức của toán học lớp 8 và được áp dụng vào rất nhiều các dạng bài tập, để hiểu hơn về tam giác đồng dạng và các trường hợp đồng dạng của tam giác hãy cùng tìm hiểu ngay trong bài viết dưới đây
Đồng dạng ở đây có nhiều cách để nhận biết, ví dụ như 2 vật thể có kích thước và hình dáng như nhau được coi là đồng dạng. Tương tự như vậy trong tam giác khái niệm đồng dạng được so sánh dựa trên hệ số của cạnh và góc
Tam giác là loại hình học phẳng gồm 3 cạnh được nối lại với nhau và được chia thành nhiều loại tùy độ dài của cạnh và vị trí. Các loại tam giác thường gặp gồm tam giác đều, tam giác cân, tam giác vuông,... Để hiểu về 2 tam giác đồng dạng ta sử dụng 2 tam giác cụ thể như sau
Tam giác ABC gọi là đồng dạng với tam giác MNP nếu:
Các góc: A = M; B = N; C = P và tỉ lệ các cạnh: BA/NM = CB/PN = CA/PM
Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
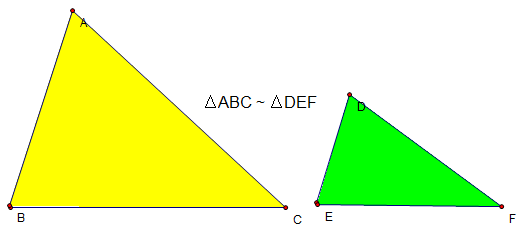
Ví dụ về 2 tam giác đồng dạng
Hai tam giác đồng dạng là một phần kiến thức của chương trình toán học phần hai tam giác đồng dạng lớp 8, trong chương trình THCS và cả THPT các bạn đều gặp rất nhiều cho nên cần nắm chắc mảng kiến thức này để phục vụ cho phần kiến thức hình học trong toán
Hai tam giác đồng dạng được chia thành 3 trường hợp đó là cạnh - cạnh - cạnh, cạnh - góc - cạnh, góc - góc - góc
Hai tam giác được gọi là đồng dạng nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia
VD: Tam giác ABC có 3 cạnh lần lượt là 6,8,10 và tam giác A’B’C’ có 3 cạnh là 3,4,5. Ta thấy 2 tam giác này có tỉ lệ 6/3=8/4=10/5 cho nên tam giác ABC và tam giác A’B’C’ là 2 tam giác đồng dạng
Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đồng dạng với nhau
VD: Tam giác MNP có MN = 3cm, NP = 4cm và góc MNP = 60 độ. Tam giác M’N’P’ có M’N’ = 6cm, N’P’ = 8cm và góc M’N’P’ = 60 độ thì 2 tam giác này đồng dạng với nhau
Trường hợp góc - góc - góc được hiểu là nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau
VD: Tam giác DEF có góc DEF = 40 độ, EDF = 50 độ và tam giác D’E’F’ có góc D’E’F’ = 40 độ, E’D’F’ = 50 độ thì 2 tam giác này được coi là đồng dạng
Bất kì các trường hợp đặc biệt của tam giác nào cũng có những tính chất khác nhau và nó cực kỳ quan trọng trong việc áp dụng để giải các bài tập hình học. Ta sẽ luôn suy ra được tính chất của 2 tam giác đồng dạng như sau
Một là tỉ số hai đường cao, hai đường phân giác, hai đường trung tuyến, hai bán kính nội tiếp và ngoại tiếp, hai chu vi tương ứng sẽ bằng tỉ số đồng dạng nếu đó là 2 tam giác đồng dạng
Hai là tỉ số diện tích của hai tam giác đồng dạng thì bằng bình phương tỉ số đồng dạng
Để chứng minh hai tam giác đồng dạng, bạn có thể áp dụng một trong bốn cách sau
4 cách chứng minh 2 tam giác đồng dạng
Cách 1: Dựa vào 1 trong 3 trường hợp đồng dạng của tam giác để chứng minh, cụ thể trong trường hợp này là cạnh - cạnh - cạnh. Hai tam giác được coi là đồng dạng nếu chúng có các cặp cạnh tương ứng tỉ lệ
Cách 2: Theo định lý Talet: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo ra trên cạnh đó những đoạn thẳng tương ứng tỷ lệ.
Cách 3: Cần chứng minh các điều kiện cần và đủ theo định nghĩa: hai tam giác có các cặp cạnh tương ứng tỷ lệ thì đồng dạng. Hai tam giác có hai cặp góc tương ứng bằng nhau thì đồng dạng, hai góc xen giữa hai cặp cạnh ấy bằng nhau thì đồng dạng
Để hiểu rõ nhất các trường hợp đồng dạng của tam giác ta cần phải bắt tay vào làm bài tập
Bài 1: Cho ΔABC cân tại A; BC = 2a. Gọi M là trung điểm của BC. Lấy lần lượt các điểm D; E trên AB; AC sao cho góc DME = góc ABC
a) Chứng minh rằng: ΔBDM ∽ ΔCME
b) Chứng minh rằng ΔMDE ∽ ΔDBM
c) Chứng minh rằng BD.CE không đổi
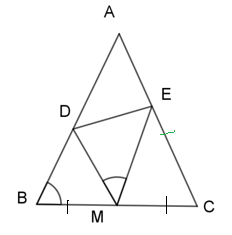
Hình minh họa bài tập 1
a) Ta có góc MBD = góc MCE vì ΔABC cân tại A (1) và góc DBM = góc DCM
(theo gt)
Mà góc DBM + góc BMD + góc MDB =180
EMD + DMB + EMC =180०
Suy ra góc BDM = góc EMC (2)
Từ (1) và (2), suy ra: ΔBDM ∽ ΔCME (g.g.g).
b) Vì ΔMDB ∽ ΔEMC
Nên BD/CM=DM/ME và BM = CM (theo gt)
BD/BM = DM/ME => ΔMDE ∽ ΔDBM.
c) Vì ΔBDM ∽ ΔCME
BD/CM = BM/CE Suy ra: CE.DB=BM.CM
Mà BM=CM=BC/2= a ⇒ BD.CE = CM.BM = a2
Bài 1: Cho tam giác vuông ABC (Â = 900) có BA = 9cm, CA = 12cm. Tia phân giác góc BAC cắt BC tại D. Kẻ DE vuông góc với AC (E thuộc AC) .
a) Tính độ dài các đoạn thẳng DB, DC, DE
b) Tính diện tích các tam giác ABD và ACD.
Bài 2: Cho hình thang ABCD (AB //CD). Biết BA = 2,5cm; DA = 3,5cm; DB = 5cm; và góc DAB = DBC.
a) Chứng minh hai tam giác ADB và BCD đồng dạng.
b) Tính độ dài các cạnh CB và CD.
Bài 3: Cho tam giác ABC vuông tại A, BA =15 cm; CA = 20 cm . Kẻ đường cao AH
a) Chứng minh: ΔABC đồng dạng ΔHBA từ đó suy ra: AB2 = BC. BH
b) Tính BH và CH.
Bài 4: Cho tam giác ABC vuông tai A, đường cao AH, biết BA = 15 cm, HA = 12cm
a) CM: ΔAHB đồng dạng ΔCHA
b) Tính các đoạn AC, HB, HC
Bài 5: Cho hình bình hành ABCD, trên tia đối của tia DA lấy AB = DM, trên tia đối của tia BA lấy NB = DA. Chứng minh:
a) ΔCBN và ΔCDM cân.
b) ΔCBN đồng dạng ΔMDC
c) Chứng minh M, C, N thẳng hàng.
Bài 6: Cho tam giác ABC (AB < AC), hai đường cao BE và CF cắt nhau tại H, đường thẳng kẻ từ B song song với CF và từ C song song với BE cắt nhau tại D. Chứng minh rằng
a) ΔABE đồng dạng ΔACF
b) AE . CB = AB . EF
c) Gọi I là trung điểm của BC. Chứng minh H, I, D thẳng hàng.
Kết luận: Như vậy qua bài viết này chắc hẳn các bạn đã nắm chắc được kiến thức hình học về hai tam giác đồng dạng cũng như các trường hợp của 2 tam giác đồng dạng. Để biết thêm những kiến thức toán học bổ ích hãy tiếp tục theo dõi các bài viết sau nhé