Trợ giúp
Học tốt trên lớp
Luyện thi
Hiểu học hành
Mang đến cho các bạn học sinh những kiến thức về đường tròn ngoại tiếp tam giác để các em có thể hiểu và làm tốt các bài tập dạng này
Đường tròn ngoại tiếp tam giác là tổng hợp các kiến thức từ khái niệm, tính chất, các kiến thức liên quan và các dạng bài tập. Giúp các bạn học sinh có thể hiểu thật rõ về đường tròn ngoại tiếp của tam giác, từ đó nắm vững các kiến thức và giải đước tất cả các bài toán về đường tròn ngoại tiếp các tam giác.
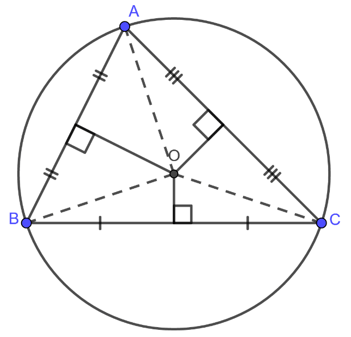
Đường tròn ngoại tiếp của một tam giác được hiểu là đường tròn tiếp xúc phía ngoài của tam giác. Vậy nên ta có định nghĩa: Đường tròn ngoại tiếp tam giác là đường tròn đi qua 3 đỉnh của một tam giác. Tâm của đường tròn ngoại tiếp của tam giác được xác định là giao điểm của 3 đường trung trực của tam giác đó. Bên cạnh, đó thì chúng ta còn có đường tròn nội tiếp tam giác sẽ tìm hiểu ở phần sau nhé.
Đường tròn ngoại tiếp tam giác còn có thể được gọi với một cái tên khác là tam giác nội tiếp đường tròn (hay tam giác nằm trong đường tròn).

Hình ảnh cụ thể về đường tròn ngoại tiếp của tam giác
Khi tiến hành nối tâm O của đường tròn với 3 đỉnh của tam giác ABC thì sẽ có được các đường thẳng : OA = OB = OC. Đó chính là bán kính của đường tròn ngoại tiếp tam giác ABC mà chúng ta cần tìm. Với công thức này, các bạn học sinh có thể áp dụng để giải quyết khá nhiều các dạng bài liên quan đến đường tròn ngoại tiếp của tam giác.
Với đường tròn ngoại tiếp tam giác sẽ có các tính chất rất quan trọng mà các bạn học sinh cần nắm thật kỹ sau đây:
Bên cạnh các kiến thức cơ bản về đường tròn ngoại tiếp tam giác. Thì các bạn học sinh cũng cần trang bị thêm cho bản thân một số kiến thức lý thuyết nâng cao về đường tròn ngoại tiếp của tam giác để có thể chinh phục được thật nhiều các dạng toán liên quan.
Để có thể xác định thật chính xác tâm của đường tròn ngoại tiếp tam giác thì các bạn học sinh cần nhớ thật kỹ kiến thức sau đây: “ Tâm của đường tròn ngoại tiếp với bất kỳ một tam giác nào luôn là giao điểm của 3 đường trung trực tam giác đó”.
Vậy nên khi muốn vẽ đường tròn ngoại tiếp của tam giác ABC thì đầu tiên chúng ta cần vẽ tam giác, tiếp đó kẻ các đường trung trực xuất phát từ 3 đỉnh của tam giác đó để có thể xác định tâm I của đường tròn. Cuối cùng chỉ cần lấy bán kính R= IA= IB= IC. Vậy là chúng ta có thể vẽ được đường tròn ngoại tiếp tam giác rồi đó.
Để có thể xác định tâm của đường tròn ngoại tiếp bất kỳ tam giác nào thì chúng ta đều cần xác định vị trí giao điểm 3 đường trung trực của tam giác đó. Ngoài ra,thì tâm của đường tròn ngoại tiếp của một tam giác cũng có thể là giao của hai đường trung trực. Vậy nên có hai cách để các bạn có thể giải quyết các bài toán dạng này thật dễ dàng.
Cách 1: Ta gọi I (x;y) là tâm của đường tròn ngoại tiếp tam giác ABC mà chúng ta cần tìm. Theo tính chất của đường tròn ngoại tiếp ta sẽ có IA = IB = IC = R. Lúc này toạ độ xác định của tâm I (x;y) sẽ là nghiệm của phương trình:
IA^2 = IB^2
IA^2 = IC^2
Cách 2: Với cách này chúng ta sẽ cần vận dụng kiến thức để viết phương trình hai đường trung trực của hai cạnh thuộc tam giác. Tiếp đó, cần xác định giao điểm của hai đường trung trực đó dựa trên những kiến thức mà chúng ta đã được học. Tâm của đường tròn ngoại tiếp tam giác chính là giao điểm của hai đường trung trực này.
Lưu ý: Với tam giác vuông thì tâm của đường tròn ngoại tiếp tam giác này chính là trung điểm của cạnh huyền. Cạnh huyền cũng chính là đường kính của đường tròn ngoại tiếp của tam giác đó.
Một số dạng toán nâng cao sẽ yêu cầu các bạn học sinh phải viết được phương trình của đường tròn ngoại tiếp tam giác. Vừa mới nghe qua thì có thể các học sinh sẽ thấy đây là một dạng bài khá khó. Tuy nhiên, chỉ cần nắm vững các bước sau đây thì việc giải bài toán này sẽ khá dễ dàng:
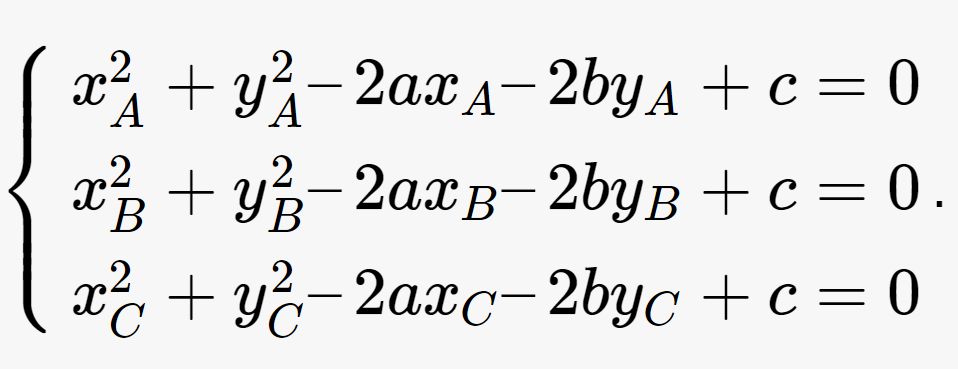
=> Sau khi giải hệ phương trình trên ta sẽ xác định được a, b, c.
Đây là dạng bài khá thường gặp trong các kỳ thi kiểm tra định kỳ. Do đó, các bạn học sinh cần nắm rõ và chi tiết cách làm sau đây để hoàn thành bài thi một cách tốt nhất.
Ví dụ: Với đề bài cho tam giác ABC có các cạnh là AB, AC và BC. Thay lần lượt các cạnh AB, AC và BC thành các ẩn a,b,c của phương trình. Ta sẽ tính được bán kính ngoại tiếp của tam giác ABC theo công thức sau:

Công thức chi tiết để tính bán kính của đường tròn ngoại tiếp của tam giác
Dưới đây, chúng tôi sẽ giới thiệu đến các bạn một số bài toán về đường tròn ngoại tiếp tam giác để các bạn hiểu và hoàn thành các bài tập một cách tốt nhất.
Bài 1: Viết phương trình đường tròn nội tiếp của tam giác ABC khi đã cho sẵn tọa độ của 3 đỉnh A(-1;3); B(5;1); C(-2;3)
Bài 2: Cho tam giác ABC đã biết A(1;3), B(-1;1), C(2;2). Tìm tọa độ của tâm đường tròn ngoại tiếp của tam giác ABC.
Bài 3: Cho tam giác ABC đều với cạnh bằng 8cm. Xác định bán kính và tâm của đường tròn ngoại tiếp của tam giác ABC?
Bài 4: Cho tam giác ABC đều với cạnh bằng 10cm. Xác định bán kính và tâm của đường tròn ngoại tiếp của tam giác ABC?
Bài 5: Cho tam giác ABC vuông tại A, và AB=6 cm, BC=8 cm,. Xác định tâm và bán kính đường tròn ngoại tiếp tam giác ABC, Tính bán kính đường tròn ngoại tiếp của tam giác bằng bao nhiêu?
Bài 6: Cho tam giác MNP có ba góc nhọn nội tiếp trong đường tròn (O; R). Ba đường của tam giác là MF, NE và PD cắt nhau tại H. Chứng minh tứ giác NDEP là tứ giác nội tiếp.
Trên đây, chúng tôi đã giúp các bạn học sinh có được tổng hợp các thông tin cần biết về đường tròn ngoại tiếp tam giác. Mong rằng với những thông tin này sẽ giúp các học sinh có thêm cho mình hành trang hữu ích cho môn toán. Đừng quên theo dõi chúng tôi để khám phá thêm thật nhiều những kiến thức toán học bổ ích nhé.