Hình Chữ Nhật Là Gì? Tính Chất, Định Nghĩa & Dấu Hiệu Nhận Biết

Các bài toán về hình học là một trong những phần cần thiết cho trẻ phát triển bộ môn toán. Trong bài viết hôm nay Clevai Math sẽ gửi tới những thông tin về hình chữ nhật là gì? tính chất, định nghĩa & dấu hiệu nhận biết cho trẻ có thể nắm bắt một cách nhanh chóng nhất. 

1. Định nghĩa về hình chữ nhật là gì?

Hình chữ nhật trong hình học Euclid là một hình tứ giác gồm có bốn góc vuông. Từ định nghĩa này, ta thấy hình chữ nhật là tứ giác lồi có bốn góc vuông, hay hình bình hành có bốn góc vuông.

Theo một định nghĩa khác thì hình chữ nhật có tên như vậy vì nó giống với các ký tự tiếng Nhật của ký tự Trung Quốc. Hình chữ nhật là tứ giác có ba góc vuông, hình thang cân có một góc vuông, hình bình hành có một góc vuông hoặc hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.

2. Tính chất hình chữ nhật

Hình chữ nhật mang  đầy đủ các tính chất của hình thang cân và hình bình hành như:

• Các cặp cạnh đối luôn song song và bằng nhau
• Các góc bằng nhau và bằng 90°
• Hai đường chéo bằng nhau và cắt nhau tại tâm 4 các cạnh bằng nhau của mỗi hàng tạo thành tam giác.
• Các đường chéo của hình chữ nhật cắt nhau và tạo thành 4 tam giác đều. Trong toán tích phân, tích phân Riemann có thể coi là giới hạn của tổng diện tích của nhiều hình chữ nhật có chiều rộng rất nhỏ.
• Nội tiếp đường tròn có tâm là tâm (giao điểm của hai đường chéo)

3. Dấu hiệu để có thể nhận biết hình chữ nhật

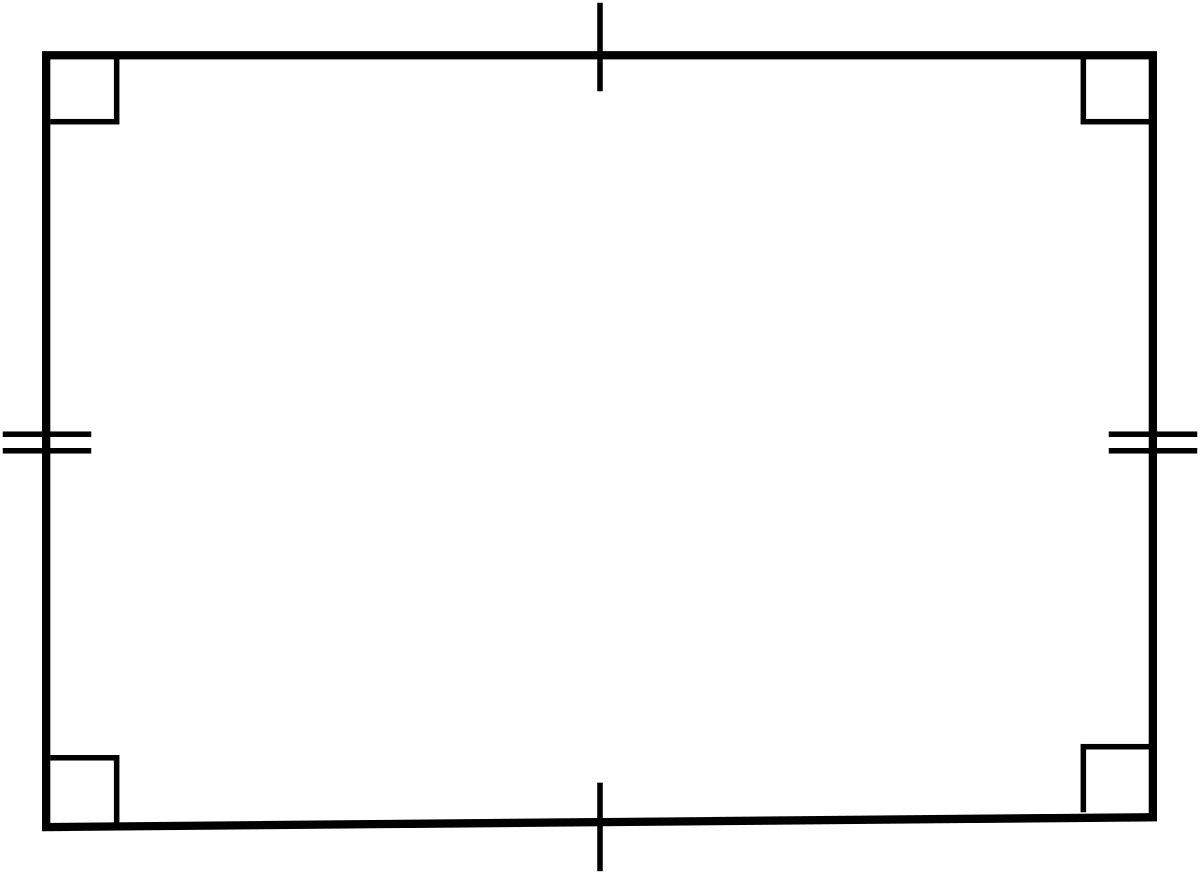
Dựa vào tính chất của hình chữ nhật, các nhà toán học đã đưa ra một số dấu hiệu nhận biết hình chữ nhật.

• Tứ giác mà có ba góc vuông là hình chữ nhật.
• Hình thang cân có một góc vuông chính là hình chữ nhật.
• Hình bình hành mà có một góc vuông là hình chữ nhật
• Mặt có hai đường chéo bằng nhau là hình chữ nhật

4. Các công thức tính toán hình chữ nhật

Các công thức liên quan đến hình chữ nhật sẽ được tổng hợp như sau:

4.1 Công thức để có thể tính chu vi hình chữ nhật

Chu vi hình chữ nhật được tính bằng tổng độ dài các đoạn thẳng bao quanh hình, cũng chính là đoạn thẳng bao quanh diện tích. Chu vi của một hình chữ nhật chính là gấp đôi tổng chiều dài và chiều rộng của nó.

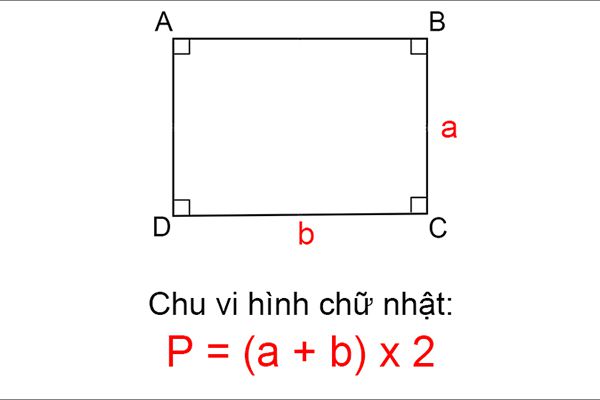
Công thức sẽ là: P=(a+b) x 2 

Trong đó: 

• a là chiều dài hình chữ nhật
• b là chiều rộng của hình chữ nhật cần tính

Ví dụ: Một thửa ruộng hình chữ nhật có chiều dài là 20m và chiều rộng là 12m. Chu vi của thửa ruộng trên sẽ bằng bao nhiêu?

Giải:

Chu vi thửa ruộng = (20+12)x2=64m

Vậy chu vi của thửa ruộng trên sẽ là 64m 

4.2 Công thức tính diện tích hình chữ nhật

Trường hợp 1: Tính diện tích hình chữ nhật khi đã biết chiều dài và chiều rộng

Diện tích hình chữ nhật bằng tích của chiều dài và chiều rộng (theo cùng đơn vị).

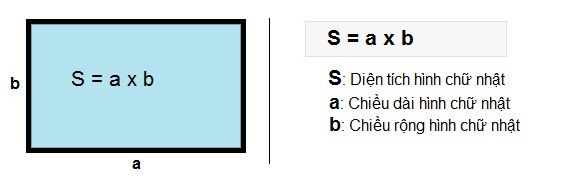
Công thức: S = a x b

Trong đó:

• a là chiều dài hình chữ nhật, 
• b chính là chiều rộng của hình chữ nhật. 
• S là diện tích hình chữ nhật. 

Ví dụ: Vẫn là thửa ruộng trên với chiều dài 20m và chiều rộng 12m. Tính diện tích thửa ruộng trên bằng bao nhiêu?

Giải

Diện tích của thửa ruộng hình chữ nhật trên sẽ bằng

S = 20 x 12 = 240 (m2)

Vậy thửa ruộng hình chữ nhật trên có diện tích bằng 240 m2

Trường hợp 2: Tính diện tích hình chữ nhật khi biết số đo một cạnh và đường chéo

Trong trường hợp này cần tính cạnh còn lại để sau đó tính diện tích hình chữ nhật theo công thức ở trường hợp 1. Giả sử bài toán là ABCD cho hình chữ nhật, biết AB = a.Đường chéo AD là c. Tính diện tích ABCD?

• Bước 1: Tính cạnh BD dựa vào định lý Pitago xét tam giác vuông ABD.
• Bước 2: Nếu tính cạnh BD, biết AB, ta được dễ dàng tính được diện tích ABCD như trường hợp 1.

Ví dụ:

Cho hình chữ nhật ABCD với chiều dài cạnh AB= 4 cm, đường chéo AC = 5 cm. Tính diện tích hình chữ nhật ABCD ở trên.

Giải

Ta có áp dụng định lý Pitago cho tam giác vuông ABC => cạnh BC có số đo là: 

BC^2 =AC^2 - AB^2 => BC^2= 25-16=9 =>BC = 3

Từ đó tính diện tích hình chữ nhật ABCD là

S=AB x BC = 4x3=12 cm2

Bài toán mở rộng

Nếu tăng chiều của một cạnh lên n lần và giữ nguyên cạnh kia thì diện tích bề mặt tăng n lần so với diện tích ban đầu.

Nếu chiều dài tăng n lần và chiều rộng tăng m lần thì thay đổi, diện tích tăng. (n x m) lần diện tích ban đầu

Lưu ý: Khi tính chu vi hoặc diện tích hình chữ nhật phải cho kích thước các cạnh của hình theo cùng một đơn vị. Nếu không thống nhất được đơn vị thì phải đổi đơn vị trước khi tính.

Clevai Math đã gửi đến quý phụ huynh và các bạn nhỏ về hình chữ nhật là gì? tính chất, định nghĩa & dấu hiệu nhận biết. Hy vọng với những thông tin trên đã giúp ích cho các bạn trong việc học tập và làm bài một cách khoa học. Mong rằng các phụ huynh sẽ giúp đỡ cho con mình luôn học tập tốt hơn.