Định Nghĩa, Chứng Minh & Tính Chất Tam Giác Cân

Tam giác cân là một trong những loại tam giác đặc biệt được ứng dụng rất nhiều trong chương trình học toán của bậc THCS lẫn THPT. Thao khả bài viết dưới đây để có thể nắm chắc kiến thức và giải bài tập một cách nhanh chóng nhé.

1. Định nghĩa tam giác cân

Tam giác có độ dài hai cạnh bằng nhau là tam giác cân. Các bộ phận của nó sẽ bao gồm:

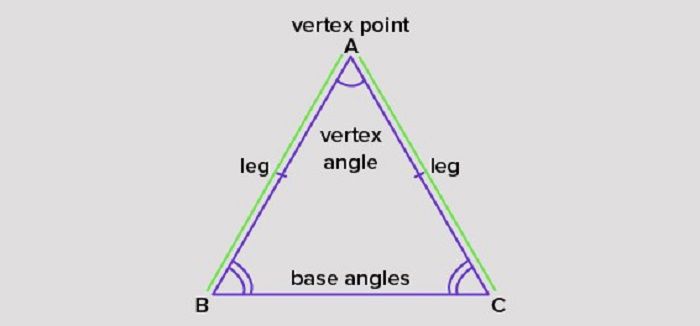
Tam giác cân có 4 bộ phận 

• Chân: Hai cạnh bằng nhau của một tam giác được coi là cân được gọi là 'chân'. Cho tam giác ABC, AB và AC là hai chân của tam giác cân.
• Đáy: 'Đáy' của một tam giác được coi là cân cân là cạnh thứ ba và không bằng nhau. Cho tam giác ABC, BC là đáy của tam giác ABC cân.
• Góc ở đỉnh: 'Góc ở đỉnh' là góc tạo bởi hai cạnh bằng nhau của một tam giác được coi là cân. ∠BAC là một góc ở đỉnh của tam giác ABC cân.
• Các góc ở đáy: 'Các góc ở đáy' là các góc bao quanh đáy của một tam giác được coi là cân. ∠ABC và ∠ACB là hai góc ở đáy của tam giác ABC cân.

Nhìn chung, tam giác được coi là cân được phân thành ba loại khác nhau:

• Tam giác nhọn cân: Tam giác nhọn cân là tam giác có cả ba góc nhỏ hơn 90° và ít nhất hai trong số các góc của nó có số đo bằng nhau. Một ví dụ về các góc của tam giác nhọn cân là 50°, 50° và 80°.
• Tam giác vuông cân: Sau đây là một ví dụ về tam giác vuông có hai cạnh (và các góc tương ứng của chúng) có số đo bằng nhau. 
• Tam giác tù cân: Tam giác tù cân là tam giác có một trong ba góc tù (nằm trong khoảng từ 90° đến 180°) và hai góc nhọn còn lại có số đo bằng nhau. Một ví dụ về góc tam giác tù cân là 30°, 30° và 120°.

2. Tính chất của tam giác cân

Mỗi hình trong hình học sẽ có một số thuộc tính làm cho nó khác biệt và độc đáo so với các hình khác. Dưới đây là một vài tính chất của tam giác được coi là cân như sau:

• Hai cạnh của tam giác bằng nhau và hai góc của tam giác bằng nhau.
• Hai cạnh bằng nhau của một tam giác được gọi là hai cạnh và góc giữa chúng gọi là góc ở đỉnh hoặc góc ở đỉnh.
• Cạnh đối diện với góc ở đỉnh gọi là đáy và các góc ở đáy bằng nhau.
• Đường vuông góc của góc ở đỉnh chia đôi đáy và góc ở đỉnh.
• Đường vuông góc vẽ từ góc ở đỉnh chia tam giác ABC cân thành hai tam giác bằng nhau và còn được gọi là đường đối xứng của nó.

Một số bài tập vận dụng cho phần này như sau:

Bài tập 1: Cho tam giác CVB cân

Hỏi: a, Tính các góc ở đáy khi biết góc ở đỉnh bằng 40 độ

        b, Tính góc ở đỉnh khi biết góc ở đáy bằng 40 độ.

Lời giải: 

a, CVB cân và C=40 độ

Ta có: C+V+B=180 độ

      Nên: C+2V=C+2B=180 độ

V = B = 180 độ – C2= 70 độ (vì B=C)

b, CVB cân, V = B =40 độ 

Ta có: C+V+B=180 độ

Nên C =180 độ – V– B =180 -2.40 =100 độ

3. Chứng minh tam giác cân

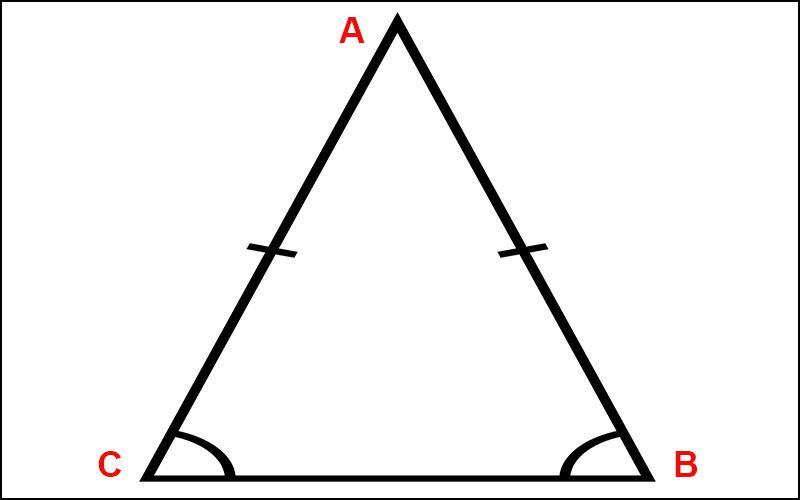
Để có thể chứng minh một tam giác bất kỳ là một tam giác được coi là cân, ta thường sử dụng các cách như sau:

• Cách thứ nhất: Chứng minh cho tam giác đó có hai cạnh bằng nhau là cách chứng minh tam giác cân thường xuyên gặp nhất. Vì cách này dùng dấu hiệu cơ bản nhất của tam giác được coi là cân để có thể biết nó cân hay không hay tam giác đó cân tại đâu. 
• Cách thứ hai: Chứng minh cho tam giác có hai góc ở đáy bằng nhau. Đây là cách chứng minh cho tam giác bất kỳ thành tam giác cân cũng khá phổ biến. Với dạng bài toán này, bạn cần phải xác định chiều dài của từng cạnh chính xác hay dùng một cạnh thứ 3 để có thể chứng minh.

Bạn có thể tham khảo các ví dụ dưới đây để học được cách chứng minh tam giác như sau:

Ví dụ 1: Trong tam giác MNP có ΔMNE = ΔMPE. Chứng minh tam giác MNP cân.

• Chứng minh theo cách 1:

Theo đề bài ra, ta có: ΔMNE = ΔMPE

Nên ⇒ MN = MP

Suy ra: Tam giác MNP cân tại M

• Chứng minh theo cách 2:

Theo đề bài ra, ta có: ΔMNE = ΔMPE

Nên ⇒ Góc N = Góc P

Suy ra: Tam giác MNP cân tại M

Ví dụ 2: Cho tam giác DEF có cạnh ED và EF bằng nhau. Kẻ EI là tia phân giác của ∠DEF.

 Hãy chứng minh rằng: Tam giác DIF cân

Bài làm:

Đầu tiên, ta xét tam giác EID và EIF có:

ED = EF 

Góc IED = Góc EIF ( Vì EI là tia phân giác của góc DEF)

Và EI là cạnh chung.

Suy ra: ΔEID =ΔEIF => ID = IF

Vậy nên tam giác DIF cân tại I.

Ví dụ 3: Cho tam giác ONM cân tại O. Lấy điểm D thuộc cạnh OM, điểm E thuộc cạnh ON sao cho OD = OE

a) Hãy so sánh góc OND và OME

b) Gọi I là giao điểm của ND và ME.  Chứng minh tam giác INM cân. Vì sao ?

Gợi ý trả lời:

a) Tam giác ONM cân tại O (giả thiết)

Nên: ON = OM và Góc ONM = Góc OMN

Xét ΔOND và ΔOME, ta có:

ON = OM (giả thiết)

Và góc O chung

OD = OE (giả thiết)

Suy ra: ΔOND = ΔOME (cạnh - góc - cạnh)

⇒  Góc OND = Góc OME ( các cặp canh tương ứng)

b) ΔINM có:

Góc INM = Góc ONM - Góc OND = Góc OMN - Góc OME = Góc IMN

Suy ra: Tam giác INM cân tại I

4. Công thức để tính diện tích của tam giác cân

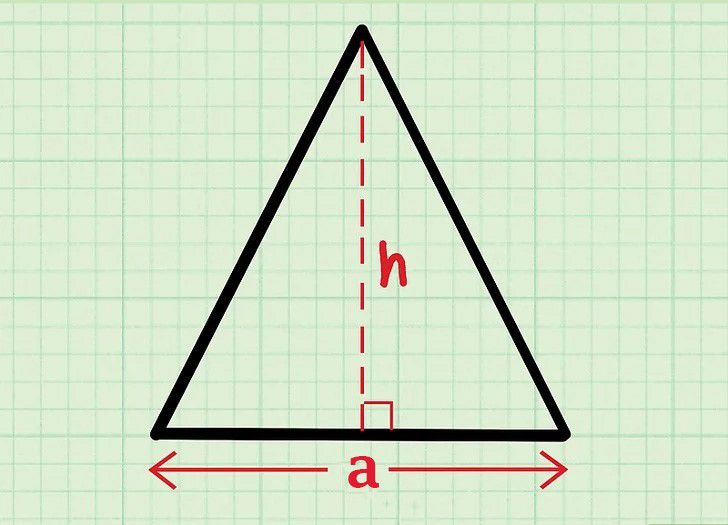
Diện tích tam giác cân là diện tích bề mặt hoặc không gian bao quanh giữa các cạnh của tam giác. Công thức diện tích tam giác nào đó cân bằng nửa tích của đáy và chiều cao của tam giác.

Công thức tính diện tích của tam giác cân chi tiết

Công thức: Diện tích tam giác cân = (cạnh đáy x chiều cao) / 2

Ví dụ 1: Tam giác NMP có chiều cao = 3cm và chiều dài đáy = 6cm thì diện tích tam giác đó sẽ là: (3 × 6) /2 = 9 cm2

Ví dụ 2: Cho tam giác EFJ vuông tại E có góc F = 45 độ, EF = 5cm. Chứng minh EFJ là vuông cân. Tính diện tích EFJ.

Bài làm: Trong tam giác EFJ có: 

Góc E + Góc F + Góc J= 180 độ 

Góc J = 180 độ – 90 độ  – 45 độ = 45 độ

Suy ra: Góc F = Góc J = 45 độ

EFJ cân tại E (1)

Vì EFJ vuông tại E (đề bài cho) (2)

Từ (1) và (2) suy ra: Tam giác EFJ vuông cân tại E.

Diện tích tam giác EFJ=12.EF.EJ = 12.5.5 = 252 (cm2) 

5. Công thức để tính chu vi của tam giác cân

Để có thể tính chu vi của tam giác cân, bạn cần phải biết chính xác đỉnh của tam giác và độ dài chính xác của 2 cạnh là được. Công thức sẽ là: P = 2a + c

Trong đó:

a: hiểu được là 2 cạnh bên của tam giác 

c: là cạnh đáy của tam giác.

Hầu hết các công thức tính chu vi tam giác bất kì cân đều có trong các câu hỏi bổ sung của nhiều bài toán yêu cầu tính diện tích tam giác. Bằng công thức có sẵn cho cả ba loại tam giác thường gặp là tam giác thường, tam giác vuông và tam giác đều. 

Như vậy, khi đã hiểu và vận dụng đúng cách tính diện tích tam giác, các em có thể sử dụng thêm các công thức xác định chu vi tam giác để nâng cao điểm số hoặc giải nhanh bài toán khi thấy phù hợp.

Ví dụ 1: Cho hình tam giác MNP cân tại N với chiều dài MN= 8 cm, MP = 6 cm. Tính chu vi của hình tam giác MNP cân đó. Dựa vào công thức tính chu vi tam giác cân ở trên, ta có cách tính như sau: P = 2 x 8 + 6 = 22 cm.

Như vậy, trên đây là toàn bộ thông tin tóm tắt liên quan đến tam giác cân, cùng với các hướng dẫn chi tiết để hoàn thành các bài toán liên quan khác nhau. Hi vọng với những thông tin hữu ích nêu trên sẽ hỗ trợ các bạn trong quá trình học tập và hoàn thành bài tập.